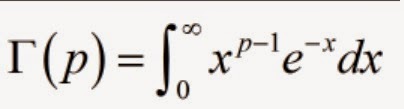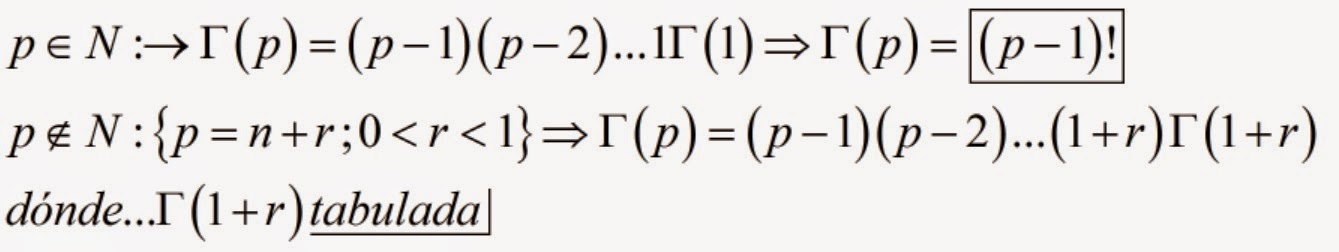Este breve y modesto compendio de lo fundamental sobre funciones eulerianas lo redacté hace treinta años formando parte de un borrador más ambicioso que comprendía un curso de cálculo integral y ecuaciones diferenciales ordinarias, con la idea de publicar un libro al respecto. La generosidad de mis tutores de doctorado. así como de eminentes profesores de Stanford demasiado por encima de mi en el aspecto profesional y científico para que me atreva a llamarlos colegas. hizo que colgara sin restricción de acceso alguna ese y otros artículos de cálculo integral y ecuaciones diferenciales así como de algunos temas de bioestadìstica, como Simulación de Montecarlo y aplicación del método Bootstrap de Efron y Tibshirani, hace unos doce en mi web (www.romanabades.com) `siguiendo la línea de comportamiento relativa al conocimiento que tan generosamente recibí. Desde entonces, al comprobar mis estadísticas, han sido miles las descargas que se han efectuado de esos materiales sin que, hasta el momento, haya modificado dicha política. Unas palabras impertinentes en comentarios me han obligado a moderarlos muy a mi pesar. Ruego a quien utilice este material para fines distintos a los de apoyo a sus estudios, al igual que yo hice en su momento, tenga a bien citar su procedencia.
1. LA FUNCIÓN "Gamma de p"
que solo tiene sentido cuando p es mayor que cero. En efecto: Descompongamos el intervalo en
Entonces:
que solo es convergente si es 1- p menor que 1 lo que implica que p sea mayor que 0.
y en el que sigue:
y en el que sigue:
es acotada.
Y mediante el cambio siguiente :
Con lo que para p=1/2 tenemos el valor para "gamma de un medio"
relacionada con la integral de las probabilidades. Integrando por partes:
2. LA FUNCIÓN "Beta de p,q"
que solo tiene sentido para p>q q>0
En particular:
Simetría
Haciendo: 1-x =y dx=-dy , vemos que resulta:
Reducción
Integrando por partes:
En particular:
 |
| (a) |
Haciendo: 1-x =y dx=-dy , vemos que resulta:
Reducción
Integrando por partes:
o sea que:
p y q de la forma n+1/2:
de dónde, si q pertenece a Z reiterando la integración
 |
| (b) |
por la simetría si es p pertenece a Z se obtiene una fórmula análoga cambiando q por p y viceversa
Relación con gamma de p y gamma de q
Multiplicando en (b) numerador y denominador por gamma de p si se cumple lo supuesto:
 |