UN ENFOQUE BREVE Y PRÁCTICO, ORIENTADO A LA RESOLUCIÓN DE LAS MISMAS, ABORDADO HACE ALGUNOS AÑOS EN MI PÁGINA WEB
Esos apuntes los redacté en 1978, durante el segundo curso de mi carrera universitaria. Posteriormente, los incorporé a mi página web. Siguiendo el ejemplo de mis mejores maestros, no los protegí en modo alguno, para que todo estudiante de la materia pudiese servirse de ellos para afianzar sus conocimientos. Posteriormente pude comprobar con disgusto que, no solo han sido profusamente copiados sin citar su procedencia, sino que incluso, en algún caso, se ha cobrado por los mismos, razón por la que ahora los he registrado.
Las ecuaciones diferenciales son aquellas en las que, en sus términos, aparecen derivadas y diferenciales.
Se llama orden de una ecuación diferencial al mayor índice de derivación que figura en ella. Por ejemplo:
son ecuaciones diferenciales lineales o de primer grado:
La primera es de segundo orden
La segunda, de primero.
Vamos a estudiar los seis tipos siguientes:
1 Variables separadas
Se caracterizan porque se puede agrupar en un miembro las x con el dx y en el otro las y con dy
Podemos considerar como forma canónica la siguiente:
que expresada en la forma:
nos permitirá obtener la solución integrando sumando a sumando y añadiéndole la constante de integración.
2 Homogéneas y reducibles a homogéneas
Consideramos de este tipo aquellas ecuaciones de forma canónica:
que permite dividir la ecuación dada por :
m es el grado de homogeneidad) con lo que quedará transformada en una ecuación de variables separables.
Se pueden reducir a ecuaciones diferenciales homogéneas las de la forma:
hallando la intersección de las rectas:
y haciendo entonces el cambio :
con lo que desaparecen los términos c y c´ y queda una ecuación homogénea
3 Exactas y Exactas factor integrante:
y , C (y)
4 Lineales de 1er Orden
( O sea: 2º miembro en y = 3º + C )
De Bernouilli
Tienen como forma canónica:
Abordamos ahora las ecuaciones diferenciales lineales de orden "n" con coeficientes constantes
5 Lineales de orden "n" con coeficientes constantes
donde se cambia y por alfa y se considera el orden de derivación como exponente, se buscan sus raices:
Por cada raíz múltiple de orden n la solución tiene un término:
multiplicado por un polinomio de grado n-1
Cada par de raíces imaginarias conjugadas múltiples de orden h, da lugar a un término de la forma :
Se caracterizan por que el segundo miembro es una función de x:
La solución general se obtiene por suma de la integral de la ecuación homogénea correspondiente y una solución particular cuya forma depende de fi de x
La solución particular será de la forma:
cuyos coeficientes se determinarán de manera que satisfagan la ecuación diferencial.
Como integral particular tomaremos:
En una entrada posterior se aplica esta teoría básica a la resolución de problemas de cada tipo de las ecuaciones diferenciales tratadas (Ver esa entrada en 4/1/2013, url: http://appelantur.blogspot.com.es/2013/01/resolucion-de-ecuaciones-diferenciales.html
|












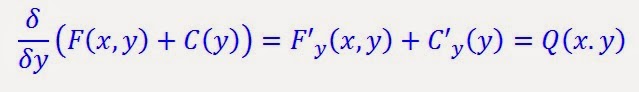













No hay comentarios:
Publicar un comentario