Consideremos dos sistemas de referencia K y K' incerciales, es decir que están en movimiento relativo. K se desplaza respecto a K' a la velocidady sentido determinados por el vector v
 Vamos a obtener las coordenadas del sistema K' referidas al sistema K, es decir la transformación de Lorentz un aparato matemático sencillo.
Vamos a obtener las coordenadas del sistema K' referidas al sistema K, es decir la transformación de Lorentz un aparato matemático sencillo.
Con la orientación indicada los ejes de abscisas coinciden constantemente. Una señal luminosa que avanza a lo largo del eje x positivo se propaga según la ecuación
 Dado que la misma señal luminosa debe propagarse también respecto a K' con la velocidad c, la ecuación para ella sería:
Dado que la misma señal luminosa debe propagarse también respecto a K' con la velocidad c, la ecuación para ella sería:
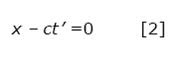 Los sucesos del espacio*tiempo que cumplen [1] también deben cumplir [2] para lo cual debe cumplirse la relación siguiente:
Los sucesos del espacio*tiempo que cumplen [1] también deben cumplir [2] para lo cual debe cumplirse la relación siguiente:
 donde lambda es una constante. Igualmente debe ocurrir con el tiempo lo que expresamos mediante la ecuación que sigue:
donde lambda es una constante. Igualmente debe ocurrir con el tiempo lo que expresamos mediante la ecuación que sigue:
 sumando y restando resèctivamente las ecuaciones [3] y [4] introduciendo (por comodidad) las constantes a y b en lugar de las λ y μ
sumando y restando resèctivamente las ecuaciones [3] y [4] introduciendo (por comodidad) las constantes a y b en lugar de las λ y μ
 se obtiene [5]
se obtiene [5] O sea que el problema está resuelto si conocemos las constantes a y b; éstas resultan de las siguientes consideraciones:
O sea que el problema está resuelto si conocemos las constantes a y b; éstas resultan de las siguientes consideraciones:
 Dado que la misma señal luminosa debe propagarse también respecto a K' con la velocidad c, la ecuación para ella sería:
Dado que la misma señal luminosa debe propagarse también respecto a K' con la velocidad c, la ecuación para ella sería: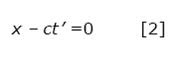 Los sucesos del espacio*tiempo que cumplen [1] también deben cumplir [2] para lo cual debe cumplirse la relación siguiente:
Los sucesos del espacio*tiempo que cumplen [1] también deben cumplir [2] para lo cual debe cumplirse la relación siguiente: donde lambda es una constante. Igualmente debe ocurrir con el tiempo lo que expresamos mediante la ecuación que sigue:
donde lambda es una constante. Igualmente debe ocurrir con el tiempo lo que expresamos mediante la ecuación que sigue: sumando y restando resèctivamente las ecuaciones [3] y [4] introduciendo (por comodidad) las constantes a y b en lugar de las λ y μ
sumando y restando resèctivamente las ecuaciones [3] y [4] introduciendo (por comodidad) las constantes a y b en lugar de las λ y μ
 se obtiene [5]
se obtiene [5] O sea que el problema está resuelto si conocemos las constantes a y b; éstas resultan de las siguientes consideraciones:
O sea que el problema está resuelto si conocemos las constantes a y b; éstas resultan de las siguientes consideraciones:
Para el origen de K' se cumple constantemente x' = 0 de manera que, por la primera de las ecuaciones [5]
 El mismo valor de v se obtiene a partir de [5] al calcular la velocidad de otro punto respecto a K, o la velocidad (dirigida hacia el eje X negativo) de un punto K'K, respecto a K'. Por tanto, es posible decir que v es la velocidad relativa de ambos sistemas. Además, por el principio de la relatividad, está claro que la longitud juzgada desde K, de una regla de medir unitaria que se halla en reposo respecto a K' tiene que ser exactamente la misma que la longitud, juzgada desde K' ,de una regla unidad que se halle en reposo respecto a K.
El mismo valor de v se obtiene a partir de [5] al calcular la velocidad de otro punto respecto a K, o la velocidad (dirigida hacia el eje X negativo) de un punto K'K, respecto a K'. Por tanto, es posible decir que v es la velocidad relativa de ambos sistemas. Además, por el principio de la relatividad, está claro que la longitud juzgada desde K, de una regla de medir unitaria que se halla en reposo respecto a K' tiene que ser exactamente la misma que la longitud, juzgada desde K' ,de una regla unidad que se halle en reposo respecto a K.Para ver qué aspecto tienen los puntos del eje X' vistos desde K ,basta con tomar una "fotografía instantánea" de K' desde K, lo cual significa dar a t (tiempo de K) un valor determinado, por ejemplo t=0
De la primera de las ecuaciones [5] se obtiene
 Así pues, dos puntos del eje X' que medidos en K' distan entre si x' = 1 tienen en nuestra instantánea la separación:
Así pues, dos puntos del eje X' que medidos en K' distan entre si x' = 1 tienen en nuestra instantánea la separación: Pero si se toma la fotografía desde K' (t' = 0), se obtiene a partir de [5] por eliminación de t y teniendo en cuenta [6]
Pero si se toma la fotografía desde K' (t' = 0), se obtiene a partir de [5] por eliminación de t y teniendo en cuenta [6] De aquí se deduce que dos puntos del eje X que distan 1 (respecto a K) tienen en nuestra instantánea la separación
De aquí se deduce que dos puntos del eje X que distan 1 (respecto a K) tienen en nuestra instantánea la separación Teniendo en cuenta lo que llevamos dicho, las dos fotografías deben ser iguales: x en [7] debe ser igual a x' en [7a] de modo que se obtiene:
Teniendo en cuenta lo que llevamos dicho, las dos fotografías deben ser iguales: x en [7] debe ser igual a x' en [7a] de modo que se obtiene: Las ecuaciones [6] y [7n] determinan las constantes a y b. Substituyendo en [5] se obtienen las ecuaciones:
Las ecuaciones [6] y [7n] determinan las constantes a y b. Substituyendo en [5] se obtienen las ecuaciones: Con ello hemos obtenido la transformación de Lorentz para sucesos localizados en el eje X; dicha transformación satisface la condición:
Con ello hemos obtenido la transformación de Lorentz para sucesos localizados en el eje X; dicha transformación satisface la condición: La extensión de este resultado a sucesos que ocurren fuera del eje X se obtiene añadiendo las relaciones:
La extensión de este resultado a sucesos que ocurren fuera del eje X se obtiene añadiendo las relaciones: Con ello se satisface el postulado de la constancia de la velocidad de la luz para rayos luminosos de dirección arbitraria, tanto para el sistema K como para el K'.
Con ello se satisface el postulado de la constancia de la velocidad de la luz para rayos luminosos de dirección arbitraria, tanto para el sistema K como para el K'.Supongamos que en el instante t=0 se emite una señal luminosa desde el origen de K. Su propagación obedece a la ecuación:
 Elevando al cuadrado:
Elevando al cuadrado: La ley de propagación de la luz , en conjunción con el postulado de la relatividad, exige que la propagación de esa misma señal, vista desde K', ocurra según la fórmula correspondiente, resultando:
La ley de propagación de la luz , en conjunción con el postulado de la relatividad, exige que la propagación de esa misma señal, vista desde K', ocurra según la fórmula correspondiente, resultando: Para que la ecuación [10a] sea consecuencia de [10] tiene que cumplirse que:
Para que la ecuación [10a] sea consecuencia de [10] tiene que cumplirse que: Puesto que la ecuación [8a] tiene que cumplirse para los puntos situados sobre el eje X, ha de ser
Puesto que la ecuación [8a] tiene que cumplirse para los puntos situados sobre el eje X, ha de ser Es fácil ver que la transformación de Lorentz cumple realmente la ecuación [11] con esta condición ,pues [11] es una consecuencia de [8a] y [9] y por tanto, también de [8] y [9]. Con ello queda derivada la transformación de Lorentz.
Es fácil ver que la transformación de Lorentz cumple realmente la ecuación [11] con esta condición ,pues [11] es una consecuencia de [8a] y [9] y por tanto, también de [8] y [9]. Con ello queda derivada la transformación de Lorentz.
Esta transformación de Lorentz, representada por [8] y [9] queda generalizada por el hecho evidente de que no es esencial que los ejes de K' se elijan espacialmente paralelos a los de K, ni tampoco que la velocidad de trslación de K' respecto a K tenga la dirección de eje X. La transformación de Lorentz, en este sentido general, cabe desglosarla como muestra un simple razonamiento en dos transformaciones, a saber: Transformaciones de Lorentz en sentido especial, y transformaciones puramente espaciales, que equivalen a la sustitución del sistema de coordenadas rectangulares por otro con ejes dirigidos en direcciones distintas.
Matemáticamente se puede caracterizar la transformación de Lorentz generalizada de la siguiente manera: Dicha transformación expresa x', y', z', t' mediante unas funciones homogéneas y lineales de x,y,z,t que hacen que la relación
 se cumpla identicamente. Lo cual quiere decir que si se substituye a la izquierda x', etc por sus expresiones en x,y,z,t, entonces el miembro izquierdo de [11a} es igual al derecho.
se cumpla identicamente. Lo cual quiere decir que si se substituye a la izquierda x', etc por sus expresiones en x,y,z,t, entonces el miembro izquierdo de [11a} es igual al derecho.
EL ESPACIO CUATRIDIMENSIONAL DE MINKOWSKY
Matemáticamente se puede caracterizar la transformación de Lorentz generalizada de la siguiente manera: Dicha transformación expresa x', y', z', t' mediante unas funciones homogéneas y lineales de x,y,z,t que hacen que la relación
 se cumpla identicamente. Lo cual quiere decir que si se substituye a la izquierda x', etc por sus expresiones en x,y,z,t, entonces el miembro izquierdo de [11a} es igual al derecho.
se cumpla identicamente. Lo cual quiere decir que si se substituye a la izquierda x', etc por sus expresiones en x,y,z,t, entonces el miembro izquierdo de [11a} es igual al derecho.EL ESPACIO CUATRIDIMENSIONAL DE MINKOWSKY
Minkowsky en 1909, es decir cuatro años después de la publicación de la teoría de la relatividad restringida, ubicó las ecuaciones de Einstein en un continuo espacio-temporal de cuatro dimensiones. Minkowski había sido profesor de Einstein y se mostró sorprendido por el talento de un alumno que había faltado a la mayoría de sus clases. Einstein, por su parte, aun cuando en principio consideró la formulación de Minkowski como un desarrollo matemático sin excesivo interés, lo cierto es que pronto le dio la importancia que tenia e influyó sin duda en su formulación de la teoría general, tratada a partir del principio de equivalencia .en la que el espacio cuatridimensional plano de Minkowski se curva por la influencia de la gravedad
En el universo de Minkowski cada suceso es un punto de coordenadas l (x,y,z,t)
Con el objeto de simplificar las representaciones se utilizan unos diagramas bidimensionales que reciben el nombre de diagramas de Minkowsky en los que se mide en abscisas la ordenada espacial x, en la que se supone se desplazan los sistemas inerciales uno respecto al otro y en ordenadas la dimensión temporal
En el universo de Minkowski cada suceso es un punto de coordenadas l (x,y,z,t)
Con el objeto de simplificar las representaciones se utilizan unos diagramas bidimensionales que reciben el nombre de diagramas de Minkowsky en los que se mide en abscisas la ordenada espacial x, en la que se supone se desplazan los sistemas inerciales uno respecto al otro y en ordenadas la dimensión temporal
 El suceso S que ocurre en el continuo espaciotemporal cuatridimensional de Minkowsky representado en el diagrama tiene por coordenadas x0 t0, denotado por S(x0, t0)
El suceso S que ocurre en el continuo espaciotemporal cuatridimensional de Minkowsky representado en el diagrama tiene por coordenadas x0 t0, denotado por S(x0, t0)Un objeto en reposo se representa por una línea vertical, lo que indica que el cuerpo evoluciona en el tiempo, manteniéndose en el mismo lugar del espacio. Para distintas posiciones espaciales en x se obtienen líneas verticales paralelas que reciben el nombre de líneas tipo tiempo. Por el contrario las líneas horizontales paralelas al eje x representan lo que llamamos líneas tipo espacio. En ellas el cuerpo está en el momento de tiempo t en distintas posiciones espaciales x.



La formulación de Minkowski resulta particularmente interesante porque facilita un medio sencillo de representar los sucesos en un continuo espacio temporal mediante un diagrama que representa en el eje de abscisas las dimensiones espaciales, de las que solo representa una, la x y en ordenadas el tiempo t. Las lineas paralelas al eje x (y lo mismo puede decirse de las y, z) representan la misma ubicacion espacial en distintos instantes de tiempo, mientras que las paralelas a t (la ordenada) representan distintas ubicaciones espaciales en un momento del tiempo. .
Esto implica que el ángulo que forma un cuerpo en movimiento con el eje t sea mayor de 45 grados y menor de 135-
El origen de un sistema inercial, evolucionando en funcion del tiempo, sigue una linea recta que se puede considerar como un observador inercial con capacidad para dar coordenadas a todos los sucesos del espacio tiempo. Esta línea recta forma un ángulo mayor de 45 grados con el eje de las x. El ángulo varia desde 90 al límite de 45 grados para el móvil avanzando en sentido positivo y desde 135 a 90 cuando se mueve en sentido contrario.


Esto implica que el ángulo que forma un cuerpo en movimiento con el eje t sea mayor de 45 grados y menor de 135-
El origen de un sistema inercial, evolucionando en funcion del tiempo, sigue una linea recta que se puede considerar como un observador inercial con capacidad para dar coordenadas a todos los sucesos del espacio tiempo. Esta línea recta forma un ángulo mayor de 45 grados con el eje de las x. El ángulo varia desde 90 al límite de 45 grados para el móvil avanzando en sentido positivo y desde 135 a 90 cuando se mueve en sentido contrario.


ESCALADO DEL EJE t
El espacio recorrido por la luz siempre será igual a su velocidad c multiplicada por el tiempo empleado. Si escalamos el eje del tiempo con la velocidad de la luz c la representación del rayo de luz de (e) será una línea de mundo de pendiente cdt/dx = c/c = 1 y, por lo que forma un ángulo de 45º con el eje x. Como ninguna velocidad puede superar la de los sucesos causa-efecto tienen líneas de mundo con inclinaciones mayores de 45º.
 Si tomamos ahora t=1, ct se convierte en c y tomamos como unidad de tiempo el “metro de tiempo” que es el tiempo que tarda la luz en recorrer un metro-
Si tomamos ahora t=1, ct se convierte en c y tomamos como unidad de tiempo el “metro de tiempo” que es el tiempo que tarda la luz en recorrer un metro-c = (espacio recorrido en un cierto intervalo de tiempo / ese intervalo de tiempo) = (1 m / 1 m) = 1 [sin dimensiones]
Cualquier velocidad se expresará como una fracción de la velocidad de la luz
CONTRACCIÓN DE LONGITUD, DILATACIÓN DEL TIEMPO, SIMULTANEIDAD
El diagrama de Minkowski nos ofrece una manera gráfica de deducir los efectos predichos por la teoría de la relatividad restringida obtenidos mediante la transformación de Lorente y es una manera gráfica y sencilla de explicarlos sin cálculo.
Sean dos hipotéticos observadores en un medio capaz de desplazarse que permanece en reposo. En un momento dado lanzan una señal luminosa dirigida al extremo delantero y trasero del mismo T y D. El rayo de luz, llega a los puntos A y B en el mismo momento t0Como puede verse en el siguiente diagrama. Las líneas punteadas forman ángulos de 450 con la abscisa x0 porque tal es la trayectoria de la luz en el diagrama hasta los extremos del vehículo A y B que tienen cada uno su correspondiente linea de espacio en el mismo momento del tiempo por estar en reposo, luego los sucesos de llegada al extremo A, trasero y B, delantero ambos a igual distancia son simultáneos o sea que están en el mismo momento del tiempo
El diagrama de Minkowski nos ofrece una manera gráfica de deducir los efectos predichos por la teoría de la relatividad restringida obtenidos mediante la transformación de Lorente y es una manera gráfica y sencilla de explicarlos sin cálculo.
Sean dos hipotéticos observadores en un medio capaz de desplazarse que permanece en reposo. En un momento dado lanzan una señal luminosa dirigida al extremo delantero y trasero del mismo T y D. El rayo de luz, llega a los puntos A y B en el mismo momento t0Como puede verse en el siguiente diagrama. Las líneas punteadas forman ángulos de 450 con la abscisa x0 porque tal es la trayectoria de la luz en el diagrama hasta los extremos del vehículo A y B que tienen cada uno su correspondiente linea de espacio en el mismo momento del tiempo por estar en reposo, luego los sucesos de llegada al extremo A, trasero y B, delantero ambos a igual distancia son simultáneos o sea que están en el mismo momento del tiempo

Supongamos ahora que el vehículo se desplaza con su ocupante mientras que el otro observador permanece en su lugar. Esto se representa en el diagrama siguiente como puede verse
 El rayo de luz, visto por el observador en reposo que permanece en el punto inicial llegará a los puntos A’ y B’ en diferentes momentos de tiempo ya que debe recorrer un mayor espacio en el sentido del movimiento representado ahora por las lineas t’. `pr el ello el segmento rB’ sobre la trayectoria de luz es mayor que el segumento rA’ siendo la velocidad de la luz la misma (razón por la que las líneas de universo de ambas siguen formando ángulo de 450 para ambos observadores sobre el eje de abscisas, mientras que los puntos A’ B’ están sobre el segmento que los une en distintos momentos del tiempo, es decir que no son simultáneos para el observador en reposo.
El rayo de luz, visto por el observador en reposo que permanece en el punto inicial llegará a los puntos A’ y B’ en diferentes momentos de tiempo ya que debe recorrer un mayor espacio en el sentido del movimiento representado ahora por las lineas t’. `pr el ello el segmento rB’ sobre la trayectoria de luz es mayor que el segumento rA’ siendo la velocidad de la luz la misma (razón por la que las líneas de universo de ambas siguen formando ángulo de 450 para ambos observadores sobre el eje de abscisas, mientras que los puntos A’ B’ están sobre el segmento que los une en distintos momentos del tiempo, es decir que no son simultáneos para el observador en reposo.Pero recordemos que el principio de inercia no distingue entre reposo o movimiento por lo que el observador en movimiento seguría observando la simultaneidad de los rayos llegando a A y a B porque sus lineas de universo respecto a su sistema de referencia siguen siendo perpendiculares en vez de oblícuas. El ve como oblicuas las del observador “en reposo” que el ve “en movimiento” de sentido contrario al suyo.
He ahí una explicación sencilla del fenómeno real de la relatividad de la simultaneidad de sucesos que nos ha brindado la técnica de los diagramas de Minkowski. con una simple representación geométrica. del fenómeno.Las líneas forman un ángulo θ que viene determinado por su velocidad que es

como puede verse en el gráfico la tangente del ángulo que forman los ejes t’ con x y también t’ con t con lo que quedan definidos los ejes de referencia del sistema S’ en movimiento relativo respecto del observador en S que son (t’, x’) como se representan a continuación:
 INTERVALO RELATIVISTA Y CALIBRACIÓN DE LOS EJES
INTERVALO RELATIVISTA Y CALIBRACIÓN DE LOS EJES
No todo es relativo al observador. La velocidad de la luz es la misma paracualquier observador. Otra cantidad que también es invariante es el intervalo entre dos sucesos, que cualquier observador puede determinara partir de sus medidas de la localización espaciotemporal de dos sucesos cualesquiera.
Supongamos que uno de los dos sucesos es el origen espaciotemporal O, coincidente para dos observadores inerciales, O y O0, y sean (x; t) y (x0; t0) las coordenadas de otro suceso A, según cada observador. El intervalo se define como
Supongamos que uno de los dos sucesos es el origen espaciotemporal O, coincidente para dos observadores inerciales, O y O0, y sean (x; t) y (x0; t0) las coordenadas de otro suceso A, según cada observador. El intervalo se define como
 El intervalo nos ayuda a calibrar los ejes: las distancias entre las marcas de referencia de los ejes de cada observador no miden lo mismo Para encontrar la relación entre las marcas de los ejes temporales (recordemos que tomamos c = 1) basta mirar donde cortan las hipérbolas t2 - x2 = 1 al eje t0, dado por t = 1 vx, pues (x = 0; t = 1) se transforma en (x0 = 0; t0 = 1).
El intervalo nos ayuda a calibrar los ejes: las distancias entre las marcas de referencia de los ejes de cada observador no miden lo mismo Para encontrar la relación entre las marcas de los ejes temporales (recordemos que tomamos c = 1) basta mirar donde cortan las hipérbolas t2 - x2 = 1 al eje t0, dado por t = 1 vx, pues (x = 0; t = 1) se transforma en (x0 = 0; t0 = 1).Para los ejes espaciales hay que mirar dónde cortan las hipérbolas t2 - x2 = 1 al eje x0, dado por t = vx, pues (x = 1; t = 0) se transforma en (x0 = 1; t0 = 0).

Los sucesos situados por encima de las líneas a 45_ guardan siempre el mismo orden temporal: se trata del cono de luz de un observador situado en el origen de coordenadas. Nótese que:Los sucesos conectados causalmente est´an separados por un intervalo positivo que llamamos tipo temporal. No hay ningún observador inercial que pueda medir sucesos separados temporalmente como sucesos simultáneos. El orden temporal de dos sucesos es el mismo para cualquier observador inercial.
Los sucesos no conectados causalmente están separados por un intervalo negativo, que llamamostipo espacial. Siempre es posible encontrar un observador inercial que pueda medir sucesos separados espacialmente como sucesos simultáneos. El orden temporal de dos sucesos depende del obervador.
Los sucesos conectados por un rayo de luz están separados por un intervalo nulo o tipo luz.
Einstein cambió radicalmente nuestro concepto de pasado, presente y futuro absolutos, introduciendo una nueva subdivisión: Para un suceso O existe elpasado (parte inferior del cono de luz), el presente (vértice del cono de luz), el futuro (parte superior del cono de luz) y el todo lo demás (exterior al cono de luz). ´ Esta ´ ultima subdivisi´on contiene a los sucesos que jamas pueden jnfluir en O y también aquéllos en los que O tampoco influirá.

UNA CONSTATACIÓN EXPERIMENTAL. LA PARADOJA DE LOS MESONES µ
Los mesones se crean en la alta atmósfera. Son inestables y su vida media es de 0.000002 segundos, Su velocidad es de 299.400 Km/s, es decir de 0.998c. Alcalzan el nivel del mar en grandes cantidades. En su vida media según la mecánica clásica solo pueden recorrer 600 metros
y = vt = 0.000002 s x 299.400 Km/s = 600 m [1]
La paradoja consiste en que para alcanzar la tierra, (lo que no solo hacen sino que penetran el suelo como está experimentalmente constatado), deben recotrrer unas diez veces esta longitud, es decir del orden de 6 Km.
DEMOSTRACIÓN DE ESTE HECHO EN EL MARCO S DEL OBSERVADOR EN TIERRALa vida media en el marco de la tierra se obtiene aplicando la transformación de Lorentz:

En este tiempo de vida útil viajando a la velocidad de 0.998c el mesón alcanza a recorrer en el sistema de referencia terrestre 9,47 Km
y = vt = 299.400 Km/s x 0,0003164 s = 9, 47 Km [3]
DEMOSTRACIÓN DEL HECHO EN EL MARCO S' DEL PROPIO MESÓN
La distancia en su propio marco de referencia, es de 600 m como la calculamos en el punto [1]. Aplicando la transformación de Lorentz al dato del recorrido en el marco S calculado en [3] vemos que coincide con lo observado en el marco S' del mesón.
 Esta distancia la recorre en su marco de referencia S' en un tiempo t' que viene dado por:
Esta distancia la recorre en su marco de referencia S' en un tiempo t' que viene dado por:
CONCLUSIÓN
Mientras que para el observador en la tierra la partícula recorre 9.740 metros en un tiempo de 0.00003164 segundos para un observador desplazándose con el mesón recorre 599 metros en 0,000002 segundos.
Se confirma que la vida de la partícula depende de las velocidades a que se mueve.
BIBLIOGRAFIA
Para la redacción del presente post se han consultado las siguientes obras:
LIBROS
- Albert Einstein; Sobre la teoría de la Relatividad Especial y General. Alianza Editorial. Madrid 2008
- Albert Einstein: El Significado de la Relatividad. Espasa Calpe. Colección Austral 2008
- Martin Gardner: La Explosión de la Relatividad. Salvat Editores 1996
- Bertrand Rusell; El ABC de la Relatividad . Ariel 1989
- Manuel Gutierrez. Introducción a la Relatividad (Departamento de Álgebra, Geometría y Topología de la Universidad de Málaga) Universidad de Málaga, Mayo 2009
- Fundación Española para la Ciencia y la Tecnología. Semana de la Ciencia 2005: La Huella de Einstein. Madrid 2005
- José Ignacio Illana. El Significado de la Relatividad (Apuntes de Clase) Universidad de Granada, 2008
- Ernesto Sabato: Uno y el Universo. Editorial Seix Barral, Colección de Bolsillo
- J. Ortega y Gasset. Meditación de la Técnica. Espasa Calpe Colección Austral. 1965
- J. Ortega y Gasset. El tema de Nuestro Tiempo (1924) Obras Completas, vol III
- J. Ortega y Gasset. La Rebelión de las Masas. Revista de Occidente, colección El Arquero, Madrid
- A.P. French. Relatividad Especial (Curso del MIT)
- David A. Santos. Multivariable Calculus Notes Philadelphia PA October 22,200
- Alvaro Tejero Cantero, Pablo Reuia Múzquiz. Ecuaciones Diferenciales Ordinarias 1.00. 13/5/2002
- Ing. Ezequiel López. M Conceptos de Relatividad Especial y General 25 de octubre de 2002
- José Mª Goicoechea Ruizgómez. Mecánica de Medios Contínuos. Resumen de Álgebra y Cálculo Tensorial
- Galileo Galilei. Sobre los dos sistemas del mundo: Ptolemáico y Copernicano
- Golovina,I. Sobre Álgebra Lineal y alguna de sus Aplicaciones. Ed. Mir Moscú 1974
WEBS Y BLOGS
- http://www.stanford.edu/dept/physics/people/faculty/susskind_leonard.html NOTA Es posible seguir las maravillosas lecciones del profesor Susskind en el canal de la Universidad de Stanford en YouTube en doce videos de aproximadamente dos horas de duración cada uno e incluso suscribirse a dicho canal
- http://fisicaymasalla.blogspot.com/ Maravilloso blog con un tratamiento riguroso, voluntariamente sencillo y muy claro y atractivo de Minkowski en el que me he basado a menudo y cuya consulta recomiendo vivamente a cualquiera que se¡ interese por el tema http://www.ugr.es/~jillana/relatividad.html
- http://abcienciade.wordpress.com/
- http://intercentres.cult.gva.es/iesleonardodavinci/fisica/fisica.htm
- http://www.acienciasgalilei.com/indicederfis.htm
- http://descartes.cnice.mec.es/index.html
- http://larelatividad.esparatodos.es/relat-a05.htm
- California Institut of Technology. El Universo Mecánico y Más Allá. Lecciones de fïsica en DVD (Pueden verse en YouTube)
- Leonard Susskind en el canal Stanford University (YouTube) sobre Relatividad. Lectures 1 a 12

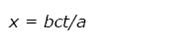
No hay comentarios:
Publicar un comentario